[전기공사기사] 4과목. 회로이론 및 제어공학
LLM을 활용한 노트로, 잘못된 정보가 있을 수 있습니다.
2022.04.24
61. 상의 순서가 a-b-c인 불평형 3상 교류회로에서 각 상의 전류가 Ia = 7.28∠15.95°(A), Ib = 12.81∠-128.66°(A), Ic = 7.21∠123.69°(A) 일 때 역상분 전류는 약 몇 A 인가?
영상전류 I0 = (Ia+Ib+Ic)/3
정상전류 I1 = (Ia + aIb + a^2Ic)/3
역상전류 I2 =(Ia+a^2Ib+aIc)/3
공학계산기로 풀면 됨.
👉 역상분 전류가 뭐야?
3상 전류가 완벽하게 균형이 맞으면 아무 문제 없이 돌아.
하지만 전압이나 전류가 불균형하면, 모터가 흔들리거나 비효율적으로 작동해.
그래서 이 불균형한 전류를 3가지 성분으로 나누는 방법이 있어!
1️⃣ 정상분( I1 ) → 원래 정상적으로 돌아야 하는 전류
2️⃣ 역상분( I2 ) → 모터를 반대 방향으로 돌리려는 전류 (우리가 찾는 값!)
3️⃣ 영상분( I0 ) → 3상이 전부 같은 방향으로 흐르는 전류
👉 역상분 전류는 어떻게 구해?
역상분 전류를 구하는 공식은 이거야:
I2=(Ia+a^2Ib+aIc)/3
여기서 "a"라는 건 120도 회전시키는 숫자야.
- a=1∠120°
- a^2=1∠240°
- a^3= 1∠360° = 1
즉, Ib를 240도 회전시키고, Ic를 120도 회전시켜서 더하는 과정이야.
👉 주어진 전류 값
각 상의 전류는 다음과 같아:
- Ia=7.28∠15.95°
- Ib=12.81∠−128.66°
- Ic=7.21∠123.69°
우선 회전 인자를 곱해보자:
- a2Ib=12.81∠(−128.66°+240°)=12.81∠111.34°
👉 값 대입하여 계산
I2=(7.28∠15.95°+12.81∠111.34°+7.21∠243.69°) / 3
이 값을 복소수로 변환한 후 더하고 다시 극좌표 형태로 변환해서 최종 답을 구할게!
계산 결과, 역상분 전류( I2 )는 약 2.51A∠96.55°입니다.
62. 그림과 같은 T형 4단자 회로의 임피던스 파라미터 Z22는?

Z11 = Z1 + Z3
Z22 = Z2 + Z3
Z12 = Z21
63.

는?

라플라스 역변환 공식
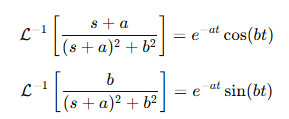

이 문제는 라플라스 역변환을 구하는 문제네요. 주어진 함수는 F(s) = (s² + 3s + 2)/(s² + 2s + 5)이고, 이걸 역변환해서 f(t)를 찾아야 하는 거죠. 그리고 보기 중에서 고르면 되는 것 같아요.
일단 라플라스 역변환을 구하는 방법을 생각해봐야겠어요. 분자와 분모가 모두 2차 다항식이네요. 보통 이런 경우에는 분모를 완전제곱식으로 바꾸거나, 부분분수 분해를 해서 처리할 수 있을 것 같아요.
먼저 분모인 s² + 2s + 5를 완전제곱식으로 변형해볼게요. s² + 2s + 1 + 4 = (s + 1)² + 4가 되네요. 이건 (s + 1)^2 + 2² 형태이므로, 지수함수와 삼각함수의 조합으로 역변환이 될 것 같아요.
분자인 s² + 3s + 2도 분모와 차수가 같기 때문에 먼저 다항식의 나눗셈을 해서 상수항과 나머지로 분리할 수 있을 거예요. 분자를 분모로 나누면 어떻게 될까요?
s² + 3s + 2 ÷ s² + 2s + 5. 이걸 계산해보면, 분자와 분모의 최고차항이 s²로 같으므로 1이 되고, 나머지는 (s² + 3s + 2) - 1*(s² + 2s + 5) = (s² + 3s + 2) - s² -2s -5 = s -3이 나옵니다. 따라서 F(s) = 1 + (s - 3)/(s² + 2s + 5)로 쓸 수 있어요.
이제 F(s) = 1 + (s - 3)/[(s + 1)^2 + 4]가 됐어요. 라플라스 역변환에서 1은 디랙 델타 함수 δ(t)에 해당하죠. 그리고 남은 부분 (s -3)/[(s + 1)^2 + 4]를 역변환해야 해요.
이 부분을 두 개의 항으로 나눌 수 있을 것 같아요. s/((s + 1)^2 + 4)와 -3/((s + 1)^2 + 4)로 나눠볼게요.
첫 번째 항은 s/((s + 1)^2 + 4)인데, 이걸 변형하려면 shift를 고려해야 해요. 일반적으로 라플라스 변환에서 e^{-at}f(t)의 변환은 F(s + a)죠. 여기서 분모가 (s + 1)^2 + 4이므로 a = 1이고, 주파수는 2인 것 같아요.
s/((s + 1)^2 + 4)를 보면, s = (s + 1) - 1로 쓸 수 있으므로, (s + 1 - 1)/[(s + 1)^2 + 4] = (s + 1)/[(s + 1)^2 + 4] - 1/[(s + 1)^2 + 4] 이렇게 분리할 수 있어요.
이제 각 항을 역변환해보면, 첫 번째 항 (s + 1)/[(s + 1)^2 + 4]는 e^{-t}cos(2t)의 라플라스 변환이죠. 왜냐하면 L{e^{-at}cos(ωt)} = (s + a)/[(s + a)^2 + ω²}이기 때문이에요. 여기서 a=1, ω=2니까 맞아요.
두 번째 항은 -1/[(s + 1)^2 + 4]인데, 이건 - (1/2) * 2/[(s + 1)^2 + 4]로 볼 수 있어요. 이는 - (1/2) e^{-t} sin(2t)가 됩니다. 왜냐하면 L{e^{-at}sin(ωt)} = ω/[(s + a)^2 + ω²}이므로, 2가 분자에 있어야 하는데 여기서는 1이므로 1/2을 곱해주는 거죠.
그래서 첫 번째 분리된 항의 역변환은 e^{-t}cos(2t) - (1/2)e^{-t}sin(2t)가 됩니다.
두 번째로 원래의 F(s)에서 (s -3) 부분을 나눴을 때 두 번째 항은 -3/((s + 1)^2 + 4)였어요. 이 역시 앞에서와 같이 -3 * (1/2) e^{-t} sin(2t)가 되겠죠. 즉, - (3/2) e^{-t} sin(2t)입니다.
이제 두 항을 합쳐보면, 첫 번째 분리된 항에서의 결과와 두 번째 항을 합치면:
e^{-t}cos(2t) - (1/2)e^{-t}sin(2t) - (3/2)e^{-t}sin(2t) = e^{-t}cos(2t) - [ (1/2 + 3/2 ) e^{-t} sin(2t) ] = e^{-t}cos(2t) - 2 e^{-t} sin(2t)
따라서 전체 F(s)의 역변환은 δ(t) + e^{-t}(cos 2t - 2 sin 2t)가 되고, 이는 보기 ③번에 해당합니다.
하지만 계산 과정에서 실수한 부분이 있는지 확인해야 해요. 특히 분자를 분리할 때 s/((s + 1)^2 + 4)를 (s + 1 -1)로 나누는 부분과 계수 계산이 정확했는지 다시 봐야겠어요.
또 다른 방법으로는 분자 s -3을 s +1 -4로 표현할 수 있어요. 즉, (s +1) -4. 그러면 (s +1)/[(s +1)^2 +4] -4/[(s +1)^2 +4]로 분리할 수 있고, 이 경우 첫 번째 항은 e^{-t}cos(2t), 두 번째 항은 -4/((s +1)^2 +4) = -4*(1/2) e^{-t} sin(2t) = -2 e^{-t} sin(2t)가 됩니다. 따라서 합치면 e^{-t}cos2t - 2 e^{-t} sin2t가 되죠. 이렇게 해도 같은 결과가 나오네요. 따라서 역변환 결과는 ③번입니다.
64. RL 직렬회로에서 시정수가 0.03s, 저항이 14.7일 때 이 회로의 인덕턴스(mH)는?
시정수 = 인덕턴스 / 저항
τ = L / R
RL 직렬회로는 저항(Resistor, R)과인덕터(Inductor, L)가 직렬로 연결된 회로입니다.
이 회로는 전류가 흐를 때 인덕터의 자기장이 변화하며 전압을 저장하거나 방출하는 특징이 있습니다.
- 저항(R): 전류의 흐름을 방해하며, 전력을 소비하는 역할을 합니다. (예: 전구, 히터)
- 인덕터(L): 자기장을 이용해 에너지를 저장하고, 전류의 급격한 변화를 방해하는 성질을 가집니다.
RL 직력회로에서 스위치를 닫아 전원을 공급하면, 인덕터는 갑자기 전류가 흐르는 것을 막으려 하므로 전류가 천천히 증가합니다. 일정 시간이 지나면 회로는 정상 상태에 도달하며, 인덕터는 단순한 도선처럼 동작합니다. 스위치를 끄면 인덕터는 자기장에 저장된 에너지를 방출하며 전류가 천천히 감소합니다.
시정수(τ)는 회로의 변화 속도를 결정하는 값으로, 전류가 안정적인 값으로 수렴하는 데 걸리는 시간을 나타냅니다.
- 시정수 τ 초가 지나면 초기값에서 (1 - 1/e) ≈ 63.2% 만큼 전류가 증가하거나 감소합니다.
- 약 5τ가 지나면 전류는 최종값의 99% 이상에 도달하여 정상 상태가 됩니다.
65. 그림과 같은 부하에 선간전압이 Vab = 100∠30°(V)인 평형 3상 전압을 가했을 때 선전류 Ia(A)는?
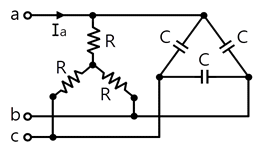
어렵다.
66. 회로에서 6Ω에 호르는 전류(A)는?
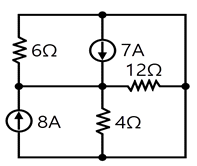
이 문제는 키르히호프의 전류 법칙(KCL)을 사용👉 "들어오는 전류의 합 = 나가는 전류의 합"
즉, 전기 흐름은 어디선가 들어오면 어딘가로 나가야 해요!
👉 이 회로에서 전류 흐름 살펴보기
- 왼쪽에서 8A가 들어옴.
- 위쪽에서 7A가 들어옴.
- 총 15A가 가운데 노드(교차점)에 모임!
이제 이 15A가 6Ω, 4Ω, 12Ω 저항을 통해 나가야 해요.
👉 저항을 통한 전류 분배
전압을 직접 구하지 않고도, 저항 비율을 이용해 전류를 분배할 수 있습니다.
노드에서 병렬로 연결된 저항들이 전압이 같기 때문에, 저항값의 역수 비율로 전류가 분배됩니다.
병렬 연결된 저항들의 전류 분배 비율:
I6Ω : I4Ω : I12Ω = 1/6 : 1/4 : 1/12 = 2 : 3 : 1
I6Ω은 즉 2 / (2 + 3 + 1) = 1 / 3 만큼 전류가 흐름
즉, 15 * 1/3 = 5A
67. 그림 (a)의 Y결선 회로를 그림 (b)의 △결선회로로 등가 변환했을 때 Rab, Rbc, Rca는 각각 몇 Ω 인가? (단, Ra = 2Ω, Rb = 3Ω, Rc = 4Ω)
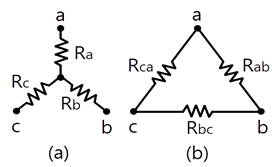
Y → Δ 변환 공식
Rab= (RaRb+RbRc+RcRa) / Rc
Rbc= (RaRb+RbRc+RcRa) / Ra
먼저, 분자를 계산해볼게요!
6+12+8=26
Rab=26/4=13/2
Rbc=26/2=13
Rca=26/3
68. 분포정수로 표현된 선로의 단위 길이당 저항이 0.5Ω/km, 인덕턴스가 1μH/km, 커패시스턴스가 6μF/km일 때 일그러짐이 없는 조건(무왜형 조건)을 만족하기 위한 단위 길이당 컨덕턴스(℧/m)는?
단위 오류로, 모두 정답처리 함. L, R, C가 모두 km로 주어졌는데, 컨덕턴스는 m로 물어봄. 따라서 10^-3을 해주는게 올바른 정답
무왜형 조건공식
LG = RC (LG전자에서 파는 RC카)
전력선이나 통신선에서 신호가 왜곡되지 않고 전달되려면, 전파 속도가 일정해야 합니다.
이를 무왜형 조건(무왜형 전송 조건, distortionless condition)이라고 합니다.
G=3×10^−3 (℧/m)
69. 회로에서 I1, I2는 아래와 같고, I3= 5.0(A), Z3 = 1.0Ω 일 때 부하(Z1, Z2, Z3) 전체에 대한 복소 전력은 약 몇 VA 인가?
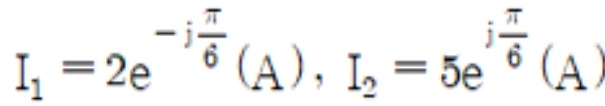
오일러 공식(Euler’s formula) 또는 공학계산기로 바로 풀어버리기
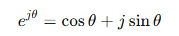
문제 풀이




70. 다음과 같은 비정현파 교류 전압 v(t)와 전류 i(t)에 의한 평균전력은 약 몇 W 인가?

비정현파 평균전력은 각 주파수 성분별 전력의 합

즉, 주어진 전압, 전류에서 + 항목별로 (VIcosθ)/2 를 수행하고 더하면 됨.
비정현파 피상전력은
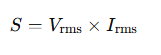
Vrms = 실효전압
Irms = 실효전류
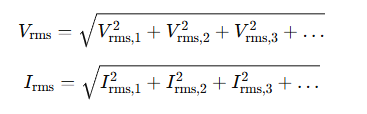
각각의 rms는 Vmax/√2
200sin100πt = 200sin(50 * 2πt)이기 때문에 V = 200, 위상 0
(1/5) sin(100πt - π/3) = (1/5) sin(50 * 2 πt - π/3)이기 때문에 I = 1/5, 위상 π/3
위상차 𝜃= 0−(−𝜋/3)=π/3
따라서 200 * 1/5 * cos( π/3) / 2 = 10 W
나머지도 이렇게 계산해서 더하면 됨
👉 비정형파란?
우리가 흔히 보는 교류 전압과 전류는 정현파(Sinusoidal Wave)라고 해. 즉, 순수한 하나의 주파수를 가진 파형이야.
하지만 비정현파(Non-Sinusoidal Wave)는 이런 순수한 정현파가 아니라, 여러 개의 주파수가 섞여 있는 파형을 말해.
예를 들어, 전압이나 전류가 기본 주파수(50Hz 또는 60Hz)뿐만 아니라 고조파(100Hz, 150Hz, 200Hz…)를 포함하고 있다면, 그건 비정현파야!
71. 다음의 논리식과 등가인 것은?
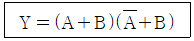
XX` = 0
XX = X
X + X` = X
X + X` = 1
값이 0, 또는 1이라고 생각하면 쉬움
72. 기본 제어요소인 비례요소의 전달함수는? (단, K는 상수이다.)
👉 전달함수
전달함수(Transfer Function) G(s)는 입력과 출력의 관계를 나타내는 수학적 표현이야.
즉, 입력 X(s)를 넣었을 때 출력 Y(s)가 어떻게 나오는지 나타내는 식이야.
G(s) = Y(s) / X(s)
👉 비례요소
비례요소(Proportional Element)는 출력이 입력에 비례하는 시스템이야. 즉 출력 Y(s)는 입력 X(s)에 K 배
Y(s) = K * X(s)
따라서 G(s) = K * X(s) / X(s) = K
73. 아래 식의 역 z 변환은?
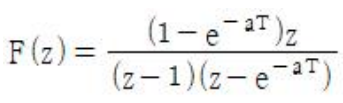

역 z 변환 공식
1/(z - a) => a^n * u(n)


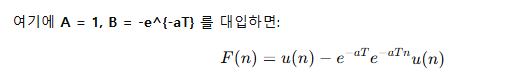
u(n)은 항상 1이므로
F(n) = 1 - e^(-aT(1 +n))
T(1 +n)을 t로 치환하면
정답 4번
👉 z 가 뭐야?
는 그냥 숫자가 아니고, 시간이 흘러가는 걸 표현하는 도구야. 좀 더 쉽게 말하면 미래로 가는 버튼 같은 거야!
예를 들어,
- z^-1는 한 칸 뒤로 가는 버튼이야.
- z^-2는 두 칸 뒤로 가는 버튼이야.
즉, z^-n은 과거의 값들을 가져오는 역할을 해!
👉 1 / (z - 1)은 뭐야?
중학교 때 배운 등비 수열에 의해
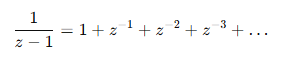
즉, 계속 뒤로 가는 버튼을 누르는 행위를 하는 식임. 근데 z^n 앞에 특정 값이 없으니 즉 *1 만 하고 있으므로
계속 값이 1이 되는 신호가 만들어짐!
👉 단위 스텝 함수 u(n) ?
은 0부터 시작해서 쭉 1이 계속 나오는 신호야. 즉,𝑛=0,1,2,3,4,... 이렇게 시간이 흐를수록 값이 계속 1이 되는 함수야.
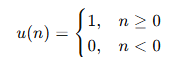
즉, 1 / (z-1) = u(n) 임
👉 z 변환
컴퓨터는 아날로그 신호(연속적인 신호)를 직접 다루지 못해. 대신 이산 신호(점으로 이루어진 신호)를 사용하지. 그런데 그냥 숫자로만 계산하면 너무 복잡하니까, 수학적으로 다루기 쉽게 변환하는 방법이 필요해. 그래서 나온 게 변환이야! 쉽게 말하면, 어떤 신호를 수학적으로 쉽게 다룰 수 있도록 변형하는 방법이라고 보면 돼.
👉 역 z 변환
변환은 신호를 다루기 쉽게 바꿨지만, 우리가 궁금한 건 최종적으로 실제 신호가 어떻게 생겼냐는 거야. 그래서 다시 원래 신호로 되돌리는 과정이 필요해. 이게 바로 역 z 변환이야!
👉 이걸 어디에 써?
이런 변환들은 디지털 신호 처리(DSP)나 디지털 제어 시스템에서 많이 써. 예를 들어, 우리가 듣는 MP3 음악도 원래 아날로그 신호를 디지털로 변환한 후 필터링해서 깨끗한 소리를 만들어. 이 과정에서 변환을 쓰고, 최종적으로 다시 원래 신호로 돌려서 음악을 듣게 되는 거야.
✅ 디지털 필터, 음성 신호 처리, 자동 제어 시스템 같은 분야에서 필수로 사용돼!
74. 다음의 상태방정식으로 표현되는 시스템의 상태천이행렬은?
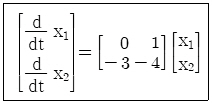
어렵다.
75. 다음 블록선도의 전달함수 (C(s)/R(s))는?
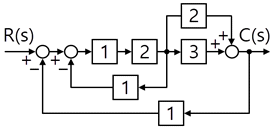
분자 = (1 * 2 * (3+2)) = 10
분모 = 1 + (1 * 2 * 1) + (1 * 2 * (3+2)) = 1 + 2 + 10 = 13
10/13
76. 제어시스템의 전달함수가 아래와 같이 표현될 때 이 시스템의 고유주파수(ωₙ(rad/s))와 감쇠율 (ζ)은?
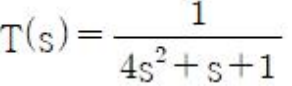
제어 시스템의 일반적인 2차 전달함수는 다음과 같은 형식입니다.
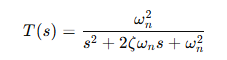
= 감쇠 진동 주파수 (Damped Frequency)
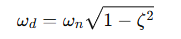
1 / (4s^2 + s + 1) 식 앞에 4 / 4 를 빼내면
(4 / 4) * ((1/4 / (s^2 + 1/4s + 1/4))
따라서 wₙ^2 = 1/4 이므로 wₙ = 1/2
2 ζwₙ = 1/4 = 2 ζ * 1/2 = ζ 이므로 ζ = 1/4
👉 고유주파수, 감쇠율은 무엇인가?
이 값들은 제어 시스템의 동적 특성을 분석하는 데 핵심적인 역할을 합니다. 쉽게 말해, 이 시스템이 얼마나 빠르게 반응하는지, 얼마나 잘 안정되는지를 나타내는 중요한 지표입니다.
👉 고유주파수(ωₙ)의 의미
ωₙ (고유주파수, Natural Frequency)는 시스템이 외부 힘이 없을 때 고유한 진동 속도를 나타냅니다.
- 값이 크면 → 빠르게 반응하는 시스템 (응답 속도가 빠름)
- 값이 작으면 → 느리게 반응하는 시스템 (응답 속도가 느림)
- 실제로 전기회로나 기계 시스템에서 응답 시간을 예측할 때 사용
👉 감쇠율(ζ)의 의미
ζ (감쇠율, Damping Ratio)는 시스템이 얼마나 빨리 진동을 멈추고 안정되는지를 나타냅니다.
- ζ > 1 (과감쇠, Overdamped) → 너무 천천히 변함 (느린 시스템, 출렁임 없이 천천히 수렴)
- ζ = 1 (임계 감쇠, Critically Damped) → 빠르게 목표 값에 도달하지만 과도한 진동 없음
- 0 < ζ < 1 (언더댐핑, Underdamped) → 목표 값에 도달하는 도중 약간 출렁거림 (오버슈트 발생)
- ζ = 0 (무감쇠, Undamped) → 진동이 멈추지 않고 계속 반복됨
👉 실제 활용 예시
- 전기 회로: 필터나 RLC 회로에서 신호가 어떻게 감쇠하는지 예측
- 로봇 제어: 로봇 팔이 목표 지점에 얼마나 빠르고 안정적으로 도달하는지 계산
- 자동차 서스펜션: 차량이 요철을 넘을 때 얼마나 출렁이는지 결정
이 문제에서 ωₙ =1/2 ζ=1/4 라는 값이 나왔는데,
- 고유주파수가 낮으니 응답 속도가 느린 시스템
- 감쇠율이 0보다 크지만 1보다 작으니 출렁거리면서(언더댐핑) 천천히 안정되는 시스템
즉, 이 시스템은 목표 값에 도달하기 전에 몇 번 진동하면서 안정될 것이라는 걸 알 수 있습니다.
이런 특성을 분석해서 시스템을 개선하거나 원하는 성능을 맞출 때 활용하는 거죠! 😊
77. 다음의 개루프 전달함수에 대한 근궤적이 실수축에서 이탈하게 되는 분리점은 약 얼마인가?
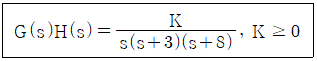
근궤적이 실수축에서 출발하다가 두 개의 경로가 갈라지는 지점을 찾아야 합니다.
이 지점을 찾는 방법은 특성 방정식을 s에 대해 미분해서 0이 되는 값을 찾는 것입니다.
역수로 만들어서 미분하면 됨.
분모를 미분하면
3s^2+22s+24=0
근의 공식에 의해 와 s=−6
👉 개루프(Open Loop)란?
제어 시스템에서 피드백(Feedback)이 없는 시스템을 개루프(Open Loop)라고 해요.
- 출력 결과를 다시 입력으로 돌려주지 않는 시스템이에요.
- 그냥 정해진 입력 → 정해진 출력만 있는 시스템이죠.
이 문제는 개루프 시스템이니까 출력 결과를 피드백하지 않고, 단순히 K값에 따라 동작하는 시스템이라는 의미입니다.
반대는 폐루프(Closed Loop)는 피드백이 있는 시스템 (출력을 보고 조절 가능)
👉 근궤적(根軌跡, Root Locus)이란?
근궤적은 제어 시스템에서 제어기의 세기를 바꿀 때(즉, K 값을 조절할 때) 시스템의 특성방정식의 해(근)가 어떻게 변하는지 나타낸 그래프예요. 쉽게 말하면, 시스템의 동작이 안정적인지, 불안정한지를 확인하는 중요한 도구예요.
💡 예시
- 자동차의 속도를 조절한다고 가정해봐요.
- 처음에는 안정적으로 잘 나가다가, 갑자기 불안정해지면 문제가 생기겠죠?
- 근궤적은 이런 변화가 어떻게 일어나는지를 보여주는 그래프예요.
👉 분리점(Breakaway Point)이란?
분리점은 근궤적에서 실수축을 따라가다가 두 개의 경로가 갈라지는 지점이에요.
💡 예시
- 길을 따라가다가 삼거리(갈림길)가 나오면 어느 방향으로 갈지 결정해야 하죠?
- 근궤적에서도 비슷한 일이 일어나요. 특정 지점에서 궤적이 나뉘어서 한쪽은 안정적으로 가고, 다른 쪽은 불안정하게 될 수도 있어요.
- 이 지점이 바로 분리점(Breakaway Point)이에요.
78. 전달함수가 아래와 같은 제어시스템에서 ω = 0.1 rad/s 일 때의 이득(dB)과 위상각(°)은 약 얼마인가?
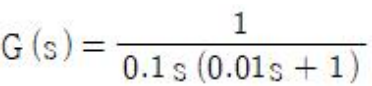
즉, s에 jω를 넣어서 크기와 위상을 구하는 문제
크기 구할 때는 마지막에 20log(N) 을 써야함
j는 허수로, 위상만을 나타내는 값임. 즉 크기 계산할때는 1로 생각하면 됨.
a + bj의 위상각은 tan^-1(b/a)로 구하면 됨. 근데 a가 0이면 무한대이므로 j만 있으면 경우 90도, -j면 있으면 -90도


👉 이득과 위상각이란
이득과 위상각은 신호(입력 vs 출력)가 어떻게 바뀌는지 나타내는 핵심 개념이에요.
- 이득(Gain, dB) → 출력 신호가 입력 신호보다 얼마나 커지거나 작아지는지 (크기 변화)
- 스피커에서 볼륨을 2배로 키운다면 → 이득 = 6 dB
- 볼륨을 10배로 키운다면 → 이득 = 20 dB
- 볼륨을 0.1배(10% 줄이면) → 이득 = -20 dB
- 위상각(Phase, °) → 출력 신호가 입력 신호보다 얼마나 늦거나 빨라지는지 (시간 차이)
- 위상각 0° → 입력과 출력이 동시에 반응 (즉, 바로 따라감)
- 위상각 90° → 반응이 늦어지지만, 아직 괜찮음
- 위상각 180° → 반응이 너무 늦어서 아예 반대로 작동할 수도 있음 (불안정!)
즉, 이득은 크기 변화, 위상각은 시간 변화를 나타내요.
👉 이득과 위상각 어디에 쓰나요?
이득과 위상각을 구하는 이유는 "시스템이 주파수 변화에 따라 어떻게 반응하는지 예측하고 조절하기 위해서"입니다.
✅ 정리하면, 이 개념은 이런 곳에서 사용됨!
- 스피커에서 특정 소리만 강조할 때 (필터)
- 드론이나 로봇이 흔들리지 않도록 균형 잡을 때 (제어 시스템)
- Wi-Fi나 5G 신호가 끊기지 않고 원활하게 전달되도록 조정할 때 (통신 시스템)
- 마이크가 주변 소음을 제거하고 사람 목소리만 또렷하게 들리도록 할 때 (노이즈 필터)
즉, 전기, 전자, 통신, 제어, 오디오 등 많은 분야에서 핵심적으로 활용되는 개념이에요! 😊
79. 그림의 신호흐름도를 미분방정식으로 표현한 것으로 옳은 것은? (단, 모든 초기 값은 0이다.)
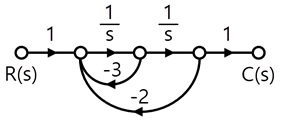
이제 그림을 보고 중요한 점을 찾자!
- R(s) → 입력 신호 (우리가 넣는 값)
- C(s) → 출력 신호 (결과)
- 1/s 박스 → 적분(∫)을 의미해!
- 적분이란? 어떤 값이 쌓이는 것!
- 예를 들어, 속도를 적분하면 위치가 나오는 것처럼!
- 화살표에 적힌 숫자들
- -3, -2 → 피드백(출력값이 다시 입력으로 들어가는 것)


80. 제어시스템의 특성방정식이 s^4+s^3-3s^2-s+2=0 와 같을 때, 이 특성방정식에서 s 평면의 오른쪽에 위치하는 근은 몇 개인가?
계산기로 근 구하여 양수의 갯수가 답.. 내 계산기는 3차까지 밖에 안된다ㅠ
계산기가 없다면 루스-후르비츠 판별법(Routh-Hurwitz Criterion)을 사용해야 함.
2022.03.05
61. 3상 평형회로에서 Y결선의 부하가 연결되어 있고, 부하에서의 선간전압이 Vab = 100√3 ∠0°(V)일 때 선전류가 Ia = 20∠-60°(A)이었다. 이 부하의 한 상의 임피던스(Ω)는? (단, 3상 전압의 상순은 a-b-c이다.)
Y결선에서는 선간전압과 상전압의 관계
상전압 = (선간전압 / √3) ∠-30
상전류 = 선전류
V = IR

62. 그림의 회로에서 120V와 30V의 전압원(능동소자)에서의 전력은 각각 몇 W인가? (단, 전압원(능동소자)에서 공급 또는 발생하는 전력은 양수(+)이고, 소비 또는 흡수하는 전력은 음수(-)이다.)
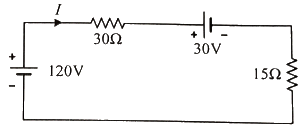
직렬 연결이므로
P = VI, V = IR, 저항은 다 더하기, 120V + 방향으로 전류가 흐르니, 30V는 전압강하니 뺴줘야 함
V = 120 - 30 = 90
R = 45
I = 90 / 45 = 2
120V가 양수방향이니 P = 120 * 2 = 240
30V는 음수방향이니 P = 30V * -2 = -60
63. 순시치 전류 i(t) = Imsin(ωt+θI)A의 파고율은 약 얼마인가?
| 전파 평균값 | 반파 평균값 | 전파 실효값 | 반파 실효값 | |
| 구형파 (사각형) | Vm (1배) | Vm/2 (0.5배) | Vm/√1 | Vm/√2 |
| 정현파 (sin, cos같은) | 2Vm/π (0.6배) | Vm/π (0.3배) | Vm/√2 | Vm/√4 |
| 삼각파 (삼각형) | Vm/2 (0.5배) | Vm/4 ( 0.25배) | Vm/√3 | Vm/√6 |
톱니파인
sin파(정현파)이므로
최대값 = Im
실효값 = Im / √2
평균값 = 2Im / π
파고율 = 최대값 / 실효값
파형율 = 실효값 / 평균값
파고율 = Im / (Im / √2) = √2 = 1.414
64. 정전용량이 C(F)인 커패시터에 단위 임펄스의 전류원이 연결되어 있다. 이 커패시터의 전압 vC(t)는? (단, u(t)는 단위 계단함수이다.)
단위 임펄스(δ(t))는 엄청 짧은 순간에 확! 전류를 주는 것이야. 이걸 콘덴서에 연결하면 어떻게 될까? 🤔
👉 콘덴서의 전압 변화
- 전류가 흐르면 콘덴서에 전기가 쌓인다
- 전류가 많으면 빨리 충전됨!
- 전류가 적으면 천천히 충전됨!
- 단위 임펄스 전류는 순간적으로 전기를 확! 밀어넣는 거야
- 그래서 전압이 갑자기 튀어오른다!
- 그리고 더 이상 전류가 안 흐르면 전압이 그대로 유지됨.
👉 결론
✔ 처음에는 0V
✔ 순간적으로 전압이 1/C
✔ 그 뒤로는 그대로 유지됨
즉, 콘덴서의 전압 Vc(t) = 1/C 만큼 점프한 후 일정하게 유지되는 그래프야!
수식으로 쓰면 Vc(t) = u(t) * 1/c
여기서 u(t)는 단위 계단 함수인데, 이건 그냥 "0초부터 갑자기 올라가서 계속 유지됨" 이라는 뜻이야
65. 그림의 회로에서 t=0s에 스위치(S)를 닫은 후 t=1s일 때 이 회로에 흐르는 전류는 약 몇 A인가?
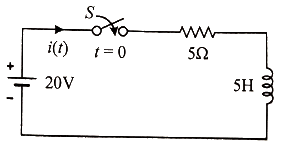
RL 직렬 회로로, 아래 4가지는 외우기
시정수(τ) = 인덕턴스 / 저항 = L / R
최대전류( I∞ ) = 전압 / 저항 = V / R
스위치를 닫을 때 시간에 따른 전류 함수 i(t) = I∞ (1 - e^(-t/ τ )
스위치를 열을 떄 시간에 다른 전류 함수 i(t) = I∞ e^(-t/ τ )
스위치를 닫을 때 시간에 따른 인덕터(L)의 𝑣𝐿(𝑡) = Ve^(-t/ τ)
vL(t)는 아래와 같이 미분식임.
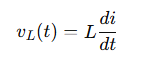
τ = 5 / 5 = 1s
I∞ = 20 / 5 = 4A
i(1) = 4 * (1 - e^(-1/1)) = 4 * (1 - e^-1)) = 4 * (1 - 0.3679) = 4 * 0.6321 = 2.52848A
66. 분포정수 회로에 있어서 선로의 단위 길이당 저항이 100Ω/m, 인덕턴스가 200mH/m, 누설컨덕턴스가 0.5℧/m일 때 일그러짐이 없는 조건(무왜형 조건)을 만족하기 위한 단위 길이당 커패시턴스는 몇 ㎌/m인가?
무왜형 조건
LG = RC
단위 문제

67. 그림의 회로가 정저항 회로가 되기 위한 L(mH)은? (단, R=10Ω, C=1000㎌이다.)
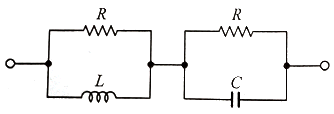
정저항 회로도 무왜형 조건인데, G = 1/R 임
LG = RC = L *(1/R) = RC = L = R^2C
10^2 * (1000 * 10^-6) = 10^2 * 10^3 * 10^-6 = 0.1H 따라서 100mH
단위 문제

정저항 회로(Resistive Matching Circuit)는 임피던스 정합(임피던스 매칭)이 이루어지는 조건을 만족하는 회로를 의미해.
즉, 주파수와 상관없이 회로의 입력 임피던스가 저항값 R과 동일하게 유지되는 조건을 찾는 거야. 이런 회로에서 조건을 만족하려면 **무왜형 조건(Distortionless Condition)**을 따라야 해.
68. 그림과 같이 3상 평형의 순저항 부하에 단상 전력계를 연결하였을 때 전력계가 W(W)를 지시하였다. 이 3상 부하에서 소모하는 전체 전력(W)는?
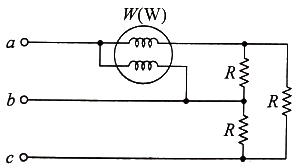
순저항 부하에서 전력계 하나만으로도 3상 전력 구하는 방법
2배...
어렵다.
69. fe(t)가 우함수이고 fo(t)가 기함수일 때 주기함수 f(t) = fe(t) + fo(t)에 대한 다음 식 중 틀린 것은?
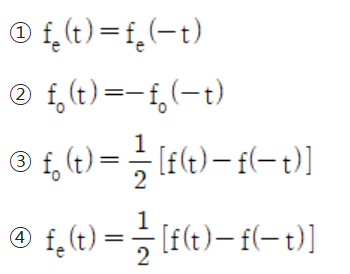
우함수 = 좌우대칭 => y = x^2
기함수 = 대각선 대칭 => y = x

70. 각 상의 전압이 다음과 같을 때 영상분 전압(V)의 순시치는? (단, 3상 전압의 상순은 a-b-c이다.)
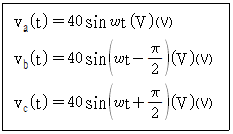
영상전압 I0 = (Va+Vb+Vc)/3
정상전압 I1 = (Va + Vb + a^2Vc)/3
역상전압 I2 =(Va+a^2Vb+aVc)/3
71. 그림의 신호흐름선도에서 전달함수 C(s)/R(s)는?
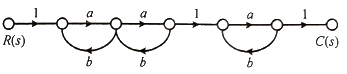

분자 = 1 * a * a * 1 * a* 1 = a^3
분모 = 1 - ((ab + ab + ab) - (abab * abab)) = 1 - 3ab + 2a^2b^2
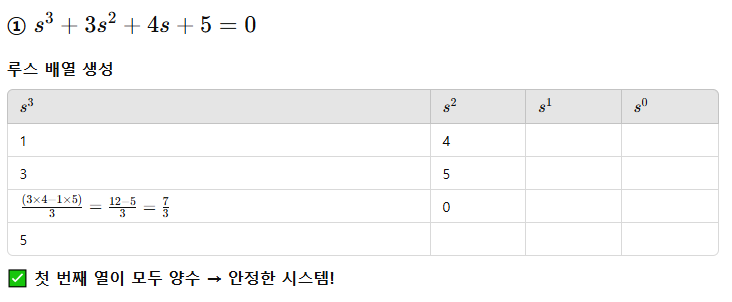
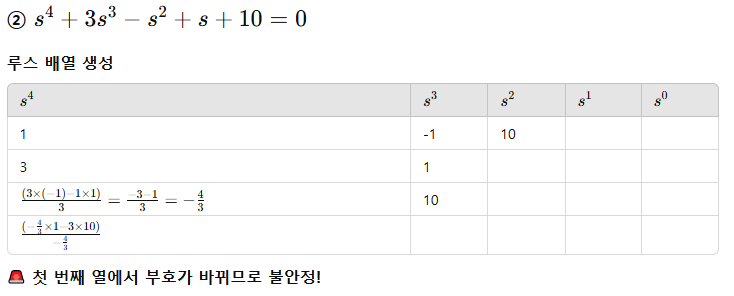
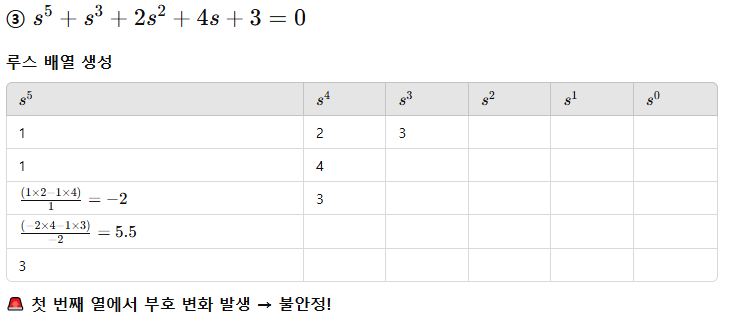
72. 다음의 특성 방정식 중 안정한 제어시스템은?

루스 배열로 풀기
73. 블록선도에서 ⓐ에 해당하는 신호는?
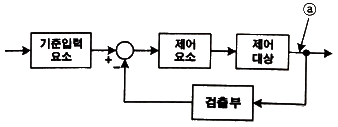
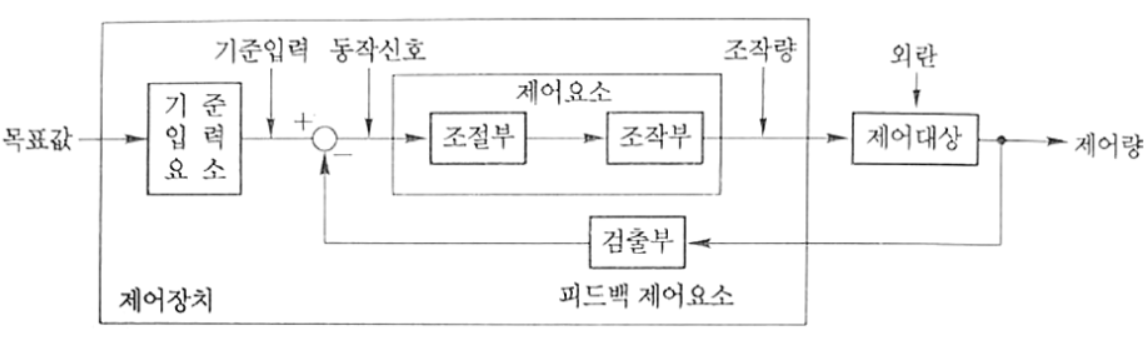
74. 그림과 같은 보드선도의 이득선도를 갖는 제어시스템의 전달함수는?
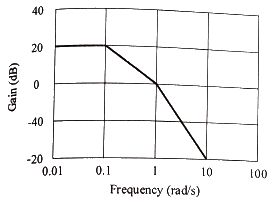
문제에 오류가 있어 모두 정답으로 함. 무엇이 오류인지는 찾지 못함.
(1) 저주파 대역에서 20 dB 일정 → 정적 이득 K
- 저주파에서 이득이 20 dB
- 따라서 20logK = 20 즉, K = 10
(2) 0.1, 1에서 꺾이므로 (s+1)(s + 0.01) 아닐까?
75. 다음의 개루프 전달함수에 대한 근궤적의 점근선이 실수축과 만나는 교차점은?
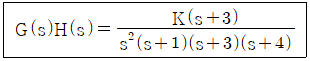
점근선이 실수축과 만나는 교차점을 중심(center, σ)이라고 함. 공식은 아래와 같음
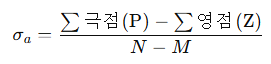
실수축에서 이탈하게 되는 분리점이랑 헷갈리지 말기. 분리점은 K를 s에 대해 미분한 값이 0이 되는 지점이 분리점임
P 각각의 극점
Z 각각의 영점
N은 극점의 개수 (분모가 0이되는)
M은 영점의 개수 (분자가 0이되는)
극점 0, 0, -1 -3 -4
영점 -3
따라서 ((0 + 0 + (-1) + (-3) + (-4)) - (-3)) / (5 - 1) = -5/4
76. 그림과 같은 블록선도의 제어시스템에 단위계단 함수가 입력되었을 때 정상상태 오차가 0.01이 되는 a의 값은?
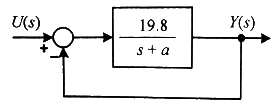
전달 함수를 구하고, 전달 함수가 T(0) = 오차율 구하면 됨

s = 0로 가정하고, G(s) / 1 + G(s) = (a / a + 19.8) = 0.01
따라서 a = 0.2
79. 다음의 미분방정식과 같이 표현되는 제어시스템이 있다. 이 제어시스템을 상태방정식 로 나타내었을 때 시스템 행렬 A는?
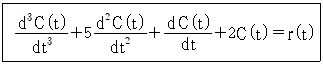
우리가 받은 문제는 3차 미분방정식이야.
근데 이대로 쓰면 너무 어려우니 이거 그냥 C(t) 대신 x1, x2,, x3 같은 이름 붙이면 엄청 쉬워져!



2021.09.21
61. 3상 평형회로에서 전압계 V, 전류계 A, 전력계 W를 그림과 같이 접속했을 때, 전압계의 지시가 100V, 전류계의 지시가 30A, 전력계의 지시 1.5㎾이었다. 이 회로에서 선간전압(Vab)과 선전류(Ia) 간의 위상차는 몇 도(°)인가? (단, 3상 전압의 상순은 a-b-c이다.)
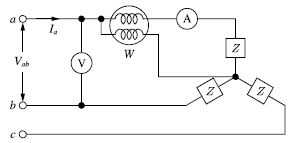
P = VIcos 이라 0.5 라고 하는데.. 너무 간단해서 아닌 것 같음.
62. 대칭 6상 성형결선 전원의 상전압의 크기가 100V일 때 이 전원의 선간접압의 크기(V)는?
성형결선은 상전압 = 선간전압
63. 무한장 무손실 전송선로의 임의의 위치에서 전압이 10V이었다. 이 선로의 인덕턴스가 10μH/m이고, 해당 위치에서 전류가 1A일 때 이 선로의 커패시턴스(㎌/m)는?
L = R^2 C 따라서 C = L / R^2
V = IR 따라서 R = V / I
R = V / I = 10
C = 10 / 10^10 = 0.1 단위 주의!
65. 그림의 회로에서 a, b 양단에 220V의 전압을 인가했을 때 전류 I가 1A이었다. 저항 R은 몇 Ω인가?
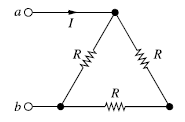
지금 회로는 삼각형(Δ) 모양으로 생겼어. 그런데, a에서 b까지 전류가 가는 길을 보면 두 개의 경로가 있어.
- 첫 번째 길: 직접 a에서 b로 가는 길 → 저항은 R
- 두 번째 길: 위쪽 꼭짓점을 거쳐서 가는 길 → 저항이 R + R = 2R이 돼
병렬 연결에서는 공식이 있어:
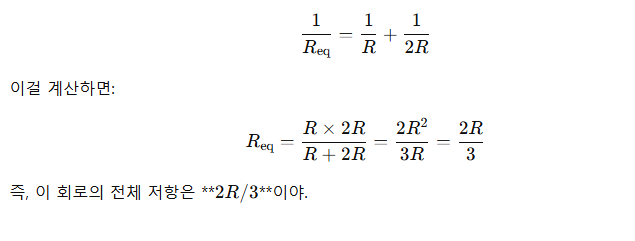

67. 다음과 같은 비정현파 교류 전압 v(t)와 전류 i(t)에 의한 평균전력 P(W)와 피상전력 Pa(VA)는 약 얼마인가?
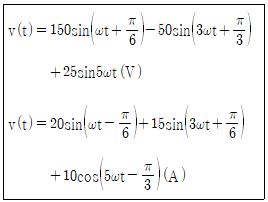
비정현파 평균전력은 각 주파수 성분별 전력의 합

즉, 주어진 전압, 전류에서 + 항목별로 (VIcosθ)/2 를 수행하고 더하면 됨.
비정현파 피상전력은
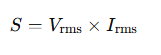
Vrms = 실효전압
Irms = 실효전류
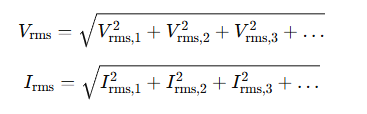
각각의 rms는 Vmax/√2
④ P=533.5, Pa=2155 이 정답인데, 계산해본 결과 P가 저렇게 나오지 않음..
70. 회로에서 인덕터의 양단 전압 VL의 크기는 약 몇 V인가? (단, V1 = 100∠0°, V2 = 100∠60°)
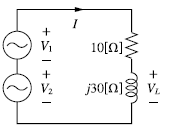
VT=V1+V2
ZT=10Ω+j30Ω=10+j30
I = V/Z 로 전체 I 구하고,
VL = I * ZL 로 구하기
71. 제어시스템의 특성방정식이 s3+11s2+2s+20 = 0와 같을 때, 이 특성방정식에서 s 평면의 오른쪽에 위치하는 근은 몇 개인가?
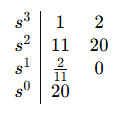
모두 양수이므로 0
72. 다음과 같은 상태방정식으로 표현되는 제어시스템에 대한 특성방정식의 근은?
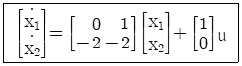
어렵다.
74. 아래 논리식과 등가인 것은?
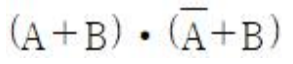
잘 모르겠으면, 0,1 을 다 넣어보자.
AA` + AB + BA` + BB = 0 + B(A + A`) + B = B + B = B
75. 다음은 근궤적의 성질(규칙)에 대한 내용의 일부를 나타낸 것이다. ( ) 안에 알맞은 내용은?

근궤적의 출발점은 개루프 전달함수의 극점이고,
근궤적의 도착점은 개루프 전달함수의 영점이다.


77. 제어시스템의 전달함수가 G(s)=e^-10s이고, 주파수가 ω=10rad/sec일 때 이 제어시스템의 이득(dB)은?
지연 시스템 G(s)=e^{-10s}은 시간 지연만 포함된 시스템입니다.
시간 지연 함수 e^{-Ts}는 크기에는 영향을 주지 않고 위상에만 영향을 미칩니다.
즉, 크기 응답은 **언제나 1(0 dB)**이고, 위상 응답만 -10ω rad 만큼 변합니다.
따라서 20log(1) = 0
78. 단위계단 함수(f(t)=u(t))의 라플라스 변환 함수 (F(s))와 z 변환 함수(F(z))는?
단위계단 함수의 라플라스 변환 F(s) = 1 / s
단위계단 함수의 z 변환 F(z) = z / (z - 1)
79. 전달함수가 아래와 같을 때 2차 제어시스템의 감쇠 진동 주파수(ωd)는 약 몇 rad/sec인가?
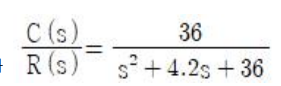
제어 시스템의 일반적인 2차 전달함수는 다음과 같은 형식입니다.
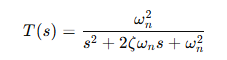
= 감쇠 진동 주파수 (Damped Frequency)
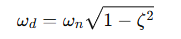
ζ = 0.35
따라서 5.62
2021.05.15
61. 정상상태에서 t=0초인 순간에 스위치 S를 열었다. 이 때 흐르는 전류 i(t)는?
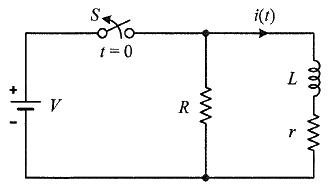
1. 스위치가 닫혀 있을 때 (t<0)
회로 동작
- 스위치 S가 닫혀 있는 상태에서는 전원이 공급되고 있습니다.
- 전류는 배터리 → R → 인덕터 L → r 경로를 따라 흐릅니다.
- 이때 인덕터는 정상 상태에서 직류 전류를 흘려주며(steady-state), 단락(Short Circuit)처럼 동작합니다.
2. 스위치를 여는 순간 (t=0)
무슨 일이 벌어질까?
- 스위치를 열면 전원이 회로에서 단절됩니다.
- 하지만 인덕터는 갑작스럽게 전류를 0으로 만들 수 없습니다!
- 이유: 인덕터의 전류 변화율은 V=Ldi/dt 에 의해 제어되며, 전류가 순간적으로 변할 수 없기 때문입니다.
- 따라서, 인덕터는 기존에 흐르던 전류를 유지하려고 합니다.
- 하지만 이제 배터리가 없기 때문에, 전류가 흐를 새로운 경로가 필요합니다.
3. 스위치를 열었을 때 회로의 변화
스위치를 열면, 전류가 흐를 수 있는 유일한 경로는 인덕터와 r이 직렬로 연결된 경로입니다.
- 이전 회로 (스위치 닫힘)
- 전원 V → 저항 R → 인덕터 → 저항 → 전원
- 스위치가 열린 후 (전원 제거됨)
- 인덕터가 방전하는 과정에서 전류가 흐를 수 있는 유일한 폐회로(closed loop)는 L과 r만 포함한 경로입니다.
- 따라서, 이제 방전 회로는 인덕터 L과 저항 r만 포함한 RL 직렬 회로가 됩니다.
즉, 스위치를 열면 전원이 사라지고, 전류는 인덕터와 내부 저항 r만을 통해 흐르게 됩니다.
따라서 초기 전류는 V/r이므로 정답은
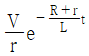
62. 파형이 톱니파인 경우 파형률은 약 얼마인가?
| 전파 평균값 | 반파 평균값 | 전파 실효값 | 반파 실효값 | |
| 구형파 (사각형) | Vm (1배) | Vm/2 (0.5배) | Vm/√1 | Vm/√2 |
| 정현파 (sin, cos같은) | 2Vm/π (0.6배) | Vm/π (0.3배) | Vm/√2 | Vm/√4 |
| 삼각파 (삼각형) | Vm/2 (0.5배) | Vm/4 ( 0.25배) | Vm/√3 | Vm/√6 |
파고율 = 최대값 / 실효값
파형율 = 실효값 / 평균값
톱니바퀴 = 삼각파
2 / /√3 = 1.155
63. 그림과 같은 함수의 라플라스 변환은?
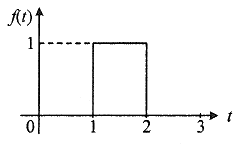
외우자
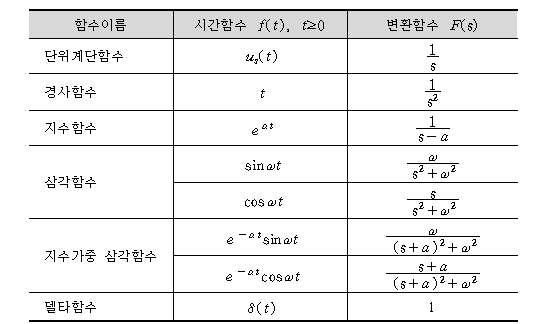


67. 회로에서 저항 1Ω에 흐르는 전류 I(A)는?
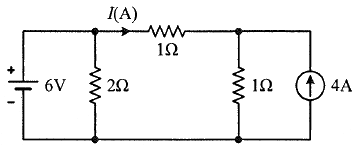
중첩의 원리는 회로에서 여러 개의 전원(전압원, 전류원)이 있을 때, 각각의 영향(전류나 전압)을 따로 계산한 후 합산하는 방법이야. 이 회로에서는 **전압원(6V)과 전류원(4A)**가 있으므로,
- 전류원을 개방(없애고 계산)하고 전압원만 고려 => 3A
- 전압원을 단락(없애고 계산)하고 전류원만 고려 => -2A
이렇게 두 경우를 각각 구해서 최종적으로 더하면 돼.
68. 그림 (a)와 같은 회로에 대한 구동점 임피던스의 극점과 영점이 각각 그림 (b)에 나타낸 것과 같고 Z(0)=1 일 때, 이 회로에서 R(Ω), L(H), C(F)의 값은?
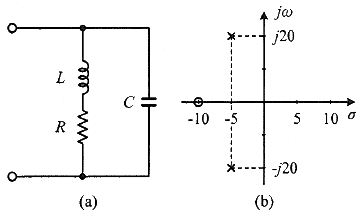
이 문제는 구동점 임피던스의 극점과 영점을 이용하여 회로 요소인 저항 R, 인덕턴스 L, 커패시턴스 값을 구하는 문제야.
하나씩 차근차근 분석해볼게.





69. 선간전압이 150V, 선전류가 10√3 A, 역률이 80%인 평형 3상 유도성 부하로 공급되는 무효전력(var)은?
무효전력 =3VIsinθ
72. 그림과 같은 제어시스템이 안정하기 위한 k의 범위는?
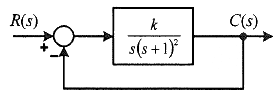

s^3+2s^2+s+k=0 루스 배열 사용해서 모두 양수이도록 하는 k를 구하자.
73. 아래와 같은 전달함수인 제어시스템의 과도 응답 특성은?
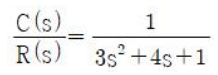
과도 응답의 유형은 시스템의 감쇠 비율( ζ\zeta, 감쇠 계수)과 관련이 있다.
- ① 무제동 (Undamped, ζ = 0)
- 극점이 순수 허수( ±jω)로 존재 → 진동하며 감쇠 없음
- ❌ 해당되지 않음.
- ② 부족제동 (Underdamped, 0<ζ<1)
- 극점이 복소수 ( −σ±jω) 형태 → 진동하며 감쇠됨
- ❌ 해당되지 않음.
- ③ 임계제동 (Critically Damped, ζ=1)
- 극점이 중근을 가짐 ( s=−α,−α) → 최소한의 지연으로 과도 응답이 감쇠
- ❌ 해당되지 않음 (현재 극점이 중근이 아님).
- ④ 과제동 (Overdamped, ζ>1)
- 극점이 서로 다른 두 개의 실근을 가짐 ( s1,s2 실수 & 음수) → 진동 없이 천천히 감쇠
- ✅ 현재 극점은 두 개의 실근을 가지므로 과제동이 맞음.
- 5. 발산 ( ζ < 0)
74. 함수 f(t) = e^-at의 z 변환 함수 F(z)는?
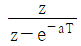

76. 전달함수가 다음과 같은 제어기가 있다. 이 제어기는 어떤 제어기인가?
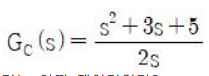
① 비례 미분 제어기
② 적분 제어기
③ 비례 적분 제어기
④ 비례 미분 적분 제어기


78. 그림의 블록선도와 같이 표현되는 제어시스템에서 A = 1, B = 1 일 때, 블록선도의 출력 C는 약 얼마인가?
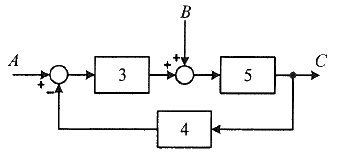
분자 = 3 * 5 + 1 * 5 = 20
분모 = 1 + 3 * 5 * 4 = 61
79. 그림과 같은 제어시스템의 폐루프 전달함수
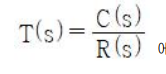
에 대한 감도 SK^T는?
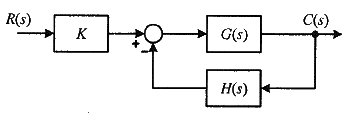
감도 = K/T * dT/dK
감도 함수는 제어 이득 K에 대한 변화가 출력 T(s)에 얼마나 영향을 미치는지를 나타내는 값이야.
T(s) = KG(s) / (1 + KG(s)H(s))

80. 다음과 같은 상태방정식으로 표현되는 제어시스템의 특성방정식의 근(s1, s2)은?
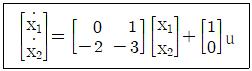
sI - A

2021.03.07
61. 블록선도와 같은 단위 피드백 제어시스템의 상태방정식은? (단, 상태변수는
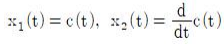
로 한다.)
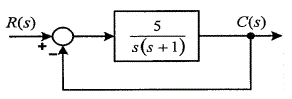
G(s)R(s) = C(s)
s^2C = C``
sC = c'
62. 적분시간 3sec, 비례 감도가 3인 비례적분동작을 하는 제어요소가 있다. 이 제어요소에 동작신호 x(t)=2t를 주었을 때 조작량은 얼마인가? (단, 초기 조작량 y(t)는 0으로 한다.)
비례적분(PI) 제어기는 입력 신호를 보고 출력을 결정하는 시스템이야.
이 제어기의 공식은:
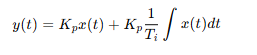
즉, 현재 입력 값도 반영하고, 과거 입력 값들의 누적(적분)도 반영해서 출력이 정해져.

69. e(t)의 z변환을 E(z)라고 했을 때 e(t)의 최종값 e(∞)은?
Z 변환의 최종값 정리(Final Value Theorem, FVT) 는 다음과 같이 표현할 수 있어:
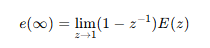
이 식은 우리가 일반적으로 알고 있는 라플라스 변환의 최종값 정리와 비슷한 개념이야.
차이가 있다면 Z 변환에서는 (1−z−1) 을 곱해서 z→1을 대입한다는 점이야.

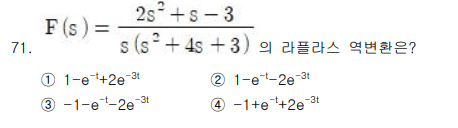

72. 전압 및 전류가 다음과 같을 때 유효전력(W) 및 역률(%)은 각각 약 얼마인가?
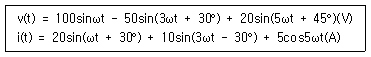
먼저 i(t) 마지막에 cos인데, sin으로 바꿔줘야 함 5sin(5wt + 90)
VICos을 이용해서 각각 모두 더하면 됨.
cos의 각도는 동일한 파의 전압과 전류의 위상차를 뺴주면 됨
실효값으로 계산해야하므로, 전압과 전류에는 각각 루트2로 나눠줘야함.
역률은 유효전력 / 피상전력
피상전력은
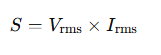
Vrms = 실효전압
Irms = 실효전류
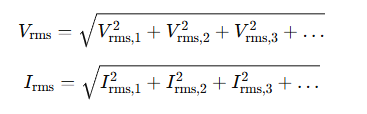
각각의 rms는 Vmax/√2
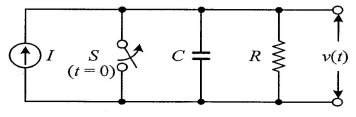
73. 회로에서 t=0초일 때 닫혀있는 스위치 S를 열었다. 이때 dv(0+)/dt의 값은? (단, C의 초기 전압은 0V이다.)
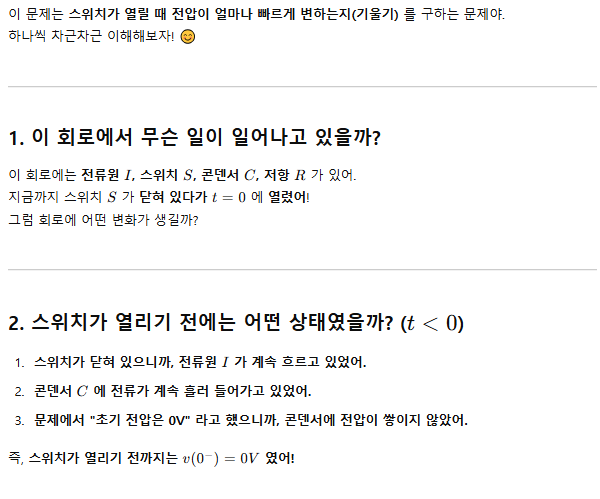



74. △ 결선된 대칭 3상 부하가 0.5Ω인 저항만의 선로를 통해 평형 3상 전압원에 연결되어 있다. 이 부하의 소비전력이 1,800W이고 역률이 0.8(지상)일 때, 선로에서 발생하는 손실이 50W이면 부하의 단자전압(V)의 크기는?
P손실 = 3 * I^2 * R
50 = 3 * I^2 * 0.5
따라서 선로전류 I = 5.77
상전류를 구해야 하므로
상전류 = 선로전류 / 루트3
따라서 상전류 = 3.33
P = 3VIcos 이므로
1800 = 3 * V * 3.33 * 0.8
따라서 V= 225
75. 그림과 같이 △ 회로를 Y 회로로 등가 변환하였을 떄 임피던스 Za(Ω)은?
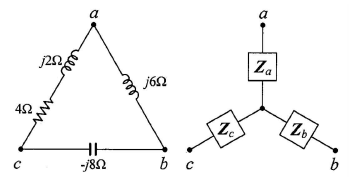
분모는 모두다 더하기 = Rab + Rbc + Rca = j6 + (-j8) + 4 + (j2) = 4
분자는 인접한 것만 곱하기 = Rab * Rca = (j6) * ( 4 + j2) = -12 + 24i
따라서 (-12 + 24i) / 4 = -3 + 6i
76. 그림과 같은 H형의 4단자 회로망에서 4단자 정수(전송 파라미터) A는? (단, V1은 입력전압이고, V2는 출력전압이고, A는 출력 개방시 회로망의 전압이득 이다.)
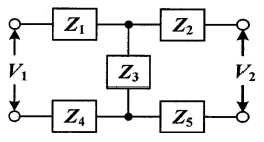
전송 행렬(ABCD 행렬)은 각 회로 요소를 행렬로 변환해서 곱하는 방식이야.
직렬 연결된 임피던스 Z
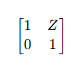
병렬 연결된 임피던스
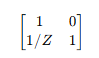
따라서 Z1Z4 직렬임피던스 * Z3병렬 * Z2Z5 직렬
77. 특성 임피던스가 400Ω인 회로 말단에 1,200Ω의 부하가 연결되어 있다. 전원측에 20kV의 전압을 인가할 때 반사파의 크기(kV)는? (단, 선로에서의 전압 감쇠는 없는 것으로 간주한다.)
반사파의 크기를 구하려면 반사계수(Reflection Coefficient) 를 먼저 계산해야 합니다. 반사계수는 다음 공식으로 구할 수 있습니다.
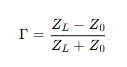

참고 추파계수는 (2 * 부파) / 부하 + 특성
따라서 (1200 - 400) / (1200 + 1600) = 0.5
V반사 = 반사각 * V입사 = 20 * 0.5 = 10
79. △ 결선된 평형 3상 부하로 흐르는 선전류가 Ia, Ib, Ic일 때 이 부하로 흐르는 영상분 전류 I0(A)는?
평형이면 Ia+Ib+Ic=0
영상전류 I0 = (Ia+Ib+Ic)/3
평형 3상 부하는 상전압과 상전류가 대칭이며, 세 선전류가 위상적으로 120°씩 어긋나 정확히 벡터합이 0이 됩니다. 즉,
Ia+Ib+Ic=0
따라서 0
80. 저항 R = 15[Ω]과 인덕턴스 L = 3[mH]를 병렬로 접속한 회로의 서셉턴스의 크기는 약 몇 [℧]인가? (단, ω = 2π × 10^5)
서셉턴스는 리액턴스의 역수
리액턴스 = wL
문제에서 요구하는 **“서셉턴스의 크기”**는 병렬로 연결된 인덕터가 갖는 리액턴스 성분에 대한 **전체 서셉턴스(=허수부)**의 절댓값입니다. 저항은 서셉턴스를 갖지 않으므로(=0) 인덕터만 고려하면 됩니다.

2020.09.26
61. RL 직렬회로에 순시치 전압 v(t) = 20 + 100sinωt + 40sin(3ωt+60°) + 40sin5ωt(V)를 가할 때 제5고조파 전류의 실효값 크기는 약 몇 A 인가? (단, R = 4Ω, ωL = 1Ω 이다.)
실효값 = 피크값 / √2
임피던스 = √(저항^2 + 리액턴스^2)
실효값 = 40 / √2
임피던스 = √(4^2 + (5*1)^2) = √41
V=IR 따라서 I = (40 / √2 )/ √41 = 4.42
62. 회로의 단자 a와 b 사이에 나타나는 전압 Vab는 몇 V 인가?
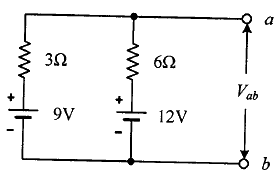
밀만의 정리
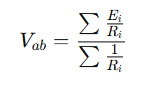
(9/3 + 12/6) / (1/3 + 1/6) = 10
밀만의 정리는 병렬 연결된 여러 개의 전압원과 저항이 있을 때, 회로의 단자 간 전압을 쉽게 구할 수 있는 방법입니다.
회로 구조 조건
- 여러 개의 전압원(전지, 배터리 등)이 병렬로 연결되어 있어야 합니다.
- 전압원 각각에 저항이 직렬로 연결되어 있어야 합니다.
- 병렬로 연결된 모든 가지(branch)는 공통된 두 개의 단자를 공유해야 합니다.
63. 그림과 같은 회로의 구동점 임피던스(Ω)는?
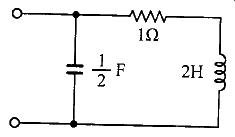
인덕터의 임피던스 ZL = sL = 2s
커패시터의 임피던스 ZC = 1/sC = 2/s
저항과 인덕터는 직렬, 커패시터는 병렬
따라서 R + L || C
1/Z = 1/(R+ZL) + 1/ZC
따라서 2(2s+1) / (2s^2 + s + 2)
64. 대칭 3상 전압이 공급되는 3상 유도전동기에서 각 계기의 지시는 다음과 같다. 유도전동기의 역률은 약 얼마인가?
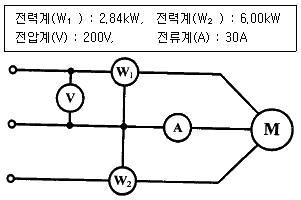
역률 = 유효전력 / 피상전력
유효전력 = W1 + W2
피상전력 = 2 √(W1^2 + W2^2 - W1W2) 또는 √3VI
유효전력 = 8.84
피상전력 = 10.4
역률 = 0.85
65. △결선으로 운전 중인 3상 변압기에서 하나의 변압기 고장에 의해 V결선으로 운전하는 경우, V결선으로 공급할 수 있는 전력은 고장 전 △결선으로 공급할 수 있는 전력에 비해 약 몇 % 인가?
△결선 = 3P
V결선 = √3P
√3 / 3 = 0.577
66. 그림의 교류 브리지 회로가 평형이 되는 조건은?
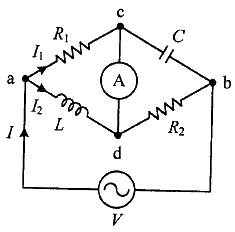
웨스톤 브리지는 Z1 * Z4 = Z2 *Z3 => 저항의 곱 = 인덕턴스(L) / 커패시턴스(C)
1. 브리지 회로의 개요
이 회로는 일반적인 웨스톤 브리지(AC 브리지) 회로 형태이며, 특정 조건에서 평형이 이루어지면 검류계(A)에 전류가 흐르지 않습니다. 즉, 검류계 전류가 0이 되는 조건을 찾으면 됩니다.
2. 브리지 평형 조건
브리지 회로에서 평형 조건이 성립하려면, 두 분기에서 임피던스 비율이 같아야 합니다. 즉, 다음 조건이 성립해야 합니다.

68. f(t) = t^n의 라플라스 변환 식은?
분모는 t의 지수보다 1 크고, 분자는 지수의 팩토리얼
n! / s^(n+1)
69. 4단자 정수 A, B, C, D 중에서 전압이득의 차원을 가진 정수는?
A 개방 전압 이득
B 단락 임피던스
C 개방 어드미턴스
D 단락 전류 이득
70. 분포정수회로에서 직렬 임피던스를 Z, 병렬어드미턴스를 Y라 할 때, 선로의 특성임피던스 Zc는?
특성임피던스 = √(직렬임피던스/병렬어드미턴스)
Zc = √(Z/Y)
특성 임피던스는 전송선(전선, 케이블 등)에서 신호가 손실 없이 잘 전달될 때의 저항값이야.
일반적인 저항(Ω)은 전류가 흐를 때 걸리는 저항을 의미하지만,
특성 임피던스는 교류(AC) 신호가 전송될 때 선로에서 나타나는 저항을 의미해.
즉, 신호가 전송될 때 전선이 얼마나 저항 역할을 하는지를 나타내는 거야.
특성 임피던스는 선로의 직렬 임피던스(Z)와 병렬 어드미턴스(Y)를 이용해서 구해:
Zc = √(Z/Y)
여기서:
- Z (직렬 임피던스): 신호가 흐를 때 선로에 포함된 저항( R )과 코일( L)의 영향을 포함해
→ Z = R + jωL - Y (병렬 어드미턴스): 선로에서 신호가 새어나가는 정도, 즉 컨덕턴스( G )와 커패시터( C )의 영향을 포함해
→ Y = G + jωC
71. e(t)의 z변환을 E(z)라고 했을 때 e(t)의 초기값 e(0)는?
라플라스 변환의 초기값 정리
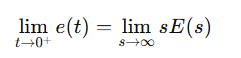
라플라스 변환의 최종값 정리
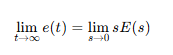
72. 폐루프 시스템에서 응답의 잔류 편차 또는 정상상태오차를 제거하기 위한 제어 기법은?
폐루프 시스템에서 응답의 잔류 편차(steady-state error) 또는 정상상태 오차를 제거하기 위한 제어 기법은 적분 제어(Integral Control) 입니다. 적분 제어(Integral Control, I 제어)는 시스템의 오차를 적분하여 보정 신호를 생성하는 방식으로, 작은 오차가 지속적으로 발생하는 경우 이를 누적하여 보상하는 역할을 합니다. 이를 통해 정상 상태에서 오차를 완전히 제거할 수 있습니다.
참고
- 비례 제어(P 제어): 현재 오차에 비례하여 출력을 조정하는 방식이지만, 정상상태 오차를 완전히 제거할 수는 없습니다.
- 미분 제어(D 제어): 오차의 변화율에 따라 출력을 조정하는 방식으로, 정상상태 오차 제거보다는 응답 속도를 향상시키는 역할을 합니다.
- PID 제어: 비례(P), 적분(I), 미분(D) 제어를 조합한 방식으로, 정상상태 오차 제거뿐만 아니라 빠른 응답성과 안정성을 확보할 수 있습니다.
73. 근궤적의 성질 중 틀린 것은?
① 근구적은 실수축을 기준으로 대칭이다.
② 점근선은 허수축 상에서 교차한다.
③ 근궤적의 가지 수는 특성방정식의 차수와 같다.
④ 근궤적은 개루프 전달함수의 극점으로부터 출발한다.
① 근궤적은 실수축을 기준으로 대칭이다.
- 맞는 설명입니다. 근궤적은 복소수 공간에서 실수축을 중심으로 대칭을 이루며 나타납니다. 이는 시스템의 특성방정식이 실수 계수를 가지므로 복소공간에서 근이 항상 켤레쌍으로 존재하기 때문입니다.
② 점근선은 허수축 상에서 교차한다.
- 틀린 설명입니다. 점근선은 시스템의 극점과 영점을 이용하여 구하며, 점근선의 교차점(점근선의 중심)은 실수축 상의 특정 위치(centroid, 중심점) 에 존재합니다.
점근선이 허수축 상에서 교차한다는 것은 잘못된 표현이며, 실제로 점근선의 중심은 다음 식으로 계산됩니다.

③ 근궤적의 가지 수는 특성방정식의 차수와 같다.
- 맞는 설명입니다. 특성방정식의 차수는 시스템의 극점 개수와 같으며, 근궤적의 가지 수도 이에 대응됩니다.
④ 근궤적은 개루프 전달함수의 극점으로부터 출발한다.
- 맞는 설명입니다. 근궤적은 개루프 전달함수의 극점(Open-loop poles)에서 시작하며, 폐루프 시스템의 극점이 어떻게 변화하는지 보여줍니다.
76. 그림과 같은 블록선도의 제어시스템에서 속도 편차 상수 Kv는 얼마인가?
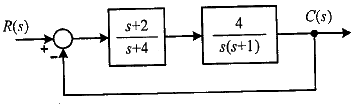
속도 편차 상수 공식
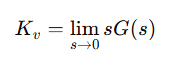
즉 sG(s) 구하고, s =0 으로
G(s) = 4(s+2) / s(s+1)(s+4)
sG(s) = 4(s+2) / (s+1)(s+4)
따라서 Kv = 4(0+2) / (0+1)(0+4) = 8/4 = 2
77. 시스템행렬 A가 다음과 같을 때 상태천이행렬을 구하면?
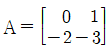
A - sI 까지해서 근은 구할 수 있겠는데, 그 다음부터는 모르겠음.
79. 전달함수가 아래와 같이 표현되는 제어시스템에서 직류 이득은 얼마인가?
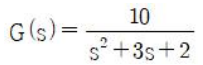
직류 이득은 G(0)을 구하는 것.
10 / 2 = 5
80. 전달함수가 아래와 같을 때 2차 제어시스템의 감쇠 진동 주파수(ωd)는 몇 rad/sec 인가?
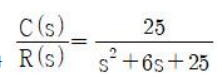
= 감쇠 진동 주파수 (Damped Frequency)
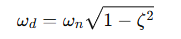
ω n = 5
ζ = 0.6
따라서 5 * 0.8 = 4
2020.08.22
61. 회로에서 20Ω의 저항이 소비하는 전력은 몇 W인가?
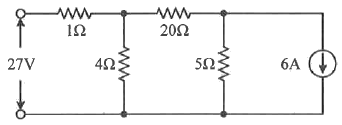
등가변환 사용
전압 -> 전류, 직렬 -> 병렬, 병렬-> 직렬
등가변환을 통해 27V를 27I로 보고, 1옴과 4옴 직렬을 병렬로 봄
1 || 4 = (1 * 4) / (1 + 4) = 0.8
따라서 27I는 다시 V = IR로 인해 V =27 * 0.8 = 21.6
오른쪽은 V = IR로 인해 V = 6 * 5 = 30
최종적으로 V1 = 21.6, V2= 30
R1 = 0.8, R2 = 20, R3 = 5가 직렬연결
따라서 I = (21.6 + 30) / (0.8 + 20 + 5) = 2
소비전력 = I^2 R = 2^2 * 20 = 80
62. 단위 길이 당 인덕턴스가 L(H/m)이고, 단위 길이 당 정전용량이 C(F/m)인 무손실 선로에서의 진행파 속도(m/S)는?
무손실 선로는 R = 0, G=0 임
이 때
진행파 속도 = 1/(√LC)
특성임피던스 = √L/C
전파정수 = ω√(LC)
63. RC 직렬회로에서 직류전압 V(V)가 인가되었을 때, 전류 i(t)에 대한 전압 방정식(KVL)이
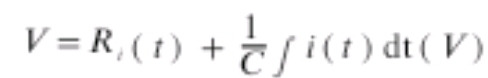
이다. 전류 i(t)의 라플라스 변환인 I(s)는? (단, C에는 초기 전하가 없다.)
V/s = RI(s) + I(s)/CS 를 풀면 됨.
66. 어떤 회로의 유효전력이 300W, 무효전력이 400var이다. 이 회로의 복소전력의 크기(VA)는?
복소전력 = 유효전력 + 무효전력i
70. R= 4Ω, ωL= 3Ω의 직렬회로에 e=100√2 sinωt+50√2 sin3ωt를 인가할 때 이 회로의 소비전력은 약 몇 W인가?
리액턴스( ωL )는 n고조파이면 n을 곱해줘야함!
전압
v1 실효값 = 100
v2 실효값 = 50
임피던스 = √(저항^2 + 리액턴스^2)
Z1 = √(4^2 + 3^2) = √25 = 5Z2 = √(4^2 + (3*3)^2) = √(16 + 81) = √91 = 9.85
전류I1 = V1/Z1 = 100/5 = 20
I2 = V2/Z2 = 50 / 9.85 = 5.07
전력
P1 = I1^2 * R = 20^2 * 4 = 1600
P2 = I2^2 * R = 5.07^2 * 4 = 103
따라서 1600 + 103 = 1703
71. 그림과 같은 피드백제어 시스템에서 입력이 단위계단함수일 때 정상상태 오차상수인 위치상수(Kp)는?
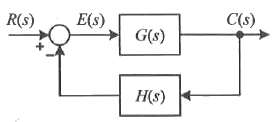
입력이 단위계단함수이므로 R = 1/s
오차는 입력과 출력의 차이이므로 오차 E = R - CH
전달함수 C/S = G / (1 + GH) 이고, 그렇다면 C = GS / (1 + GH)
오차 E = R - CH에 C를 변경하면
E = R - (GSH / (1 + GH) = R / (1 + GH) 임
그리고 R = 1/s 이므로 E = 1 / (s(1+GH)) 임
정상상태 오차 최종값 정리에 의해
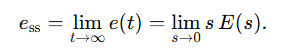
E를 변경하면
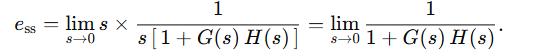
오차상수는 1 / 1 +Kp 형태이므로 Kp 가 GH 임.
따라서 정답은
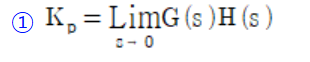
72. 다음 회로에서 입력 전압 v1(t)에 대한 출력 전압 v2(t)의 전달함수 G(s)는?
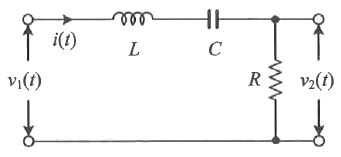
전달함수 G(s) = v2(s) / v1(s)
Z = sL + 1/sC + R
i(s) = v1(s) / Z
전류는 동일하고 저항 R에 걸리는 최종 전압이 출력 v2이므로
v2(s) = i(s) * R
따라서 v2(s) = R * v1(s) / Z
G(s) = v2(s) / v1(s) = R*v1(s) / Z / v1(s) = R / Z = R / (sL + 1/sC + R) = sRC / (s^2LC + 1 + RsC)
76. 특성방정식의 모든 근이 s평면(복소평면)의 jw축(허수축)에 있을 때 이 제어시스템의 안정도는?
안정한 시스템: 모든 근이 왼쪽 반평면(실수부가 음수)에 있을 때 시스템은 안정합니다.
불안정한 시스템: 하나라도 오른쪽 반평면(실수부가 양수)에 근이 존재하면 시스템은 불안정합니다.
경계 안정(marginally stable): 모든 근이 jw축 위에 있으며, 실수부가 정확히 0일 때, 시스템은 발산하지 않지만 특정 초기 조건에서는 진동할 수 있습니다.
s-평면은 제어 시스템의 동작을 분석하는 공간이야.
이걸 쉽게 설명하면, 시간 영역(time domain)이 아니라, 주파수와 성분을 분석하는 영역이라고 생각하면 돼.
수학적으로는 s = σ + jω 라고 표현하는데,
- σ(시그마, 실수부): 감쇠(damping)를 나타냄 → 시스템이 안정한지 불안정한지를 결정
- jω(제이 오메가, 허수부): 진동(oscillation) 성분을 나타냄 → 시스템이 주파수적으로 어떻게 반응하는지 보여줌
즉, s-평면은 "어떤 시스템이 시간이 지나면서 어떻게 변하는지"를 분석하는 특수한 좌표평면이야.
물에 떠 있는 공의 움직임을 생각해보자!
- 왼쪽 반평면 (σ < 0, 안정한 시스템)
- 물 위에서 공을 톡 치면, 점점 움직임이 줄어들고 결국 가만히 멈춤 (진동이 감쇠됨)
- 오른쪽 반평면 (σ > 0, 불안정한 시스템)
- 물 위에서 공을 톡 치면, 점점 더 크게 움직이면서 난리가 남 (점점 더 진동이 커짐 → 폭발적인 불안정성)
- jw축 위에 있음 (σ = 0, 경계 안정 시스템)
- 물 위에서 공을 톡 치면, 계속 똑같은 크기로 움직이면서 진동 (감쇠도 없고, 폭발도 없음)
즉, jw축에 근이 있다는 건 시스템이 계속 같은 크기로 진동만 하고, 멈추거나 폭발하지 않는 상태를 의미해.
이걸 경계 안정(Marginally Stable) 상태라고 불러.
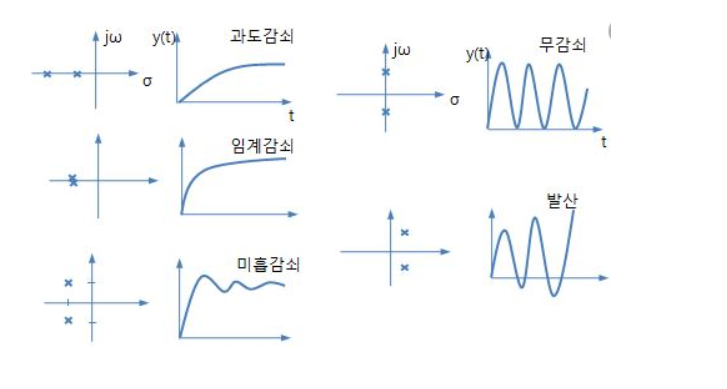
77. 어떤 제어시스템의 개루프 이득이
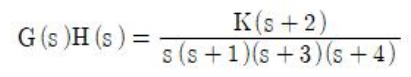
일 때 이 시스템이 가지는 근궤적의 가지(branch) 수는?
근궤적의 가지 수 = 특성방정식(분모)의 차수